“ 在人类历史的长河中,真理因为像黄金一样重,总是沉于河底而很难被人发现,相反地,那些牛粪一样轻的谬误倒漂浮在上面到处泛滥。 —— 培根 ”
算法原理
参考阮一峰博客 字符串匹配的Boyer-Moore算法
- 父
HERE IS A SIMPLE EXAMPLE,子EXAMPLE。
-
子字符串与父子符串头部对齐,从尾部开始比较。如果最后一个字符对不上,那么父子符串前面的整体上一定不是待搜索的字符串,我们把这个对不上的字符S称为坏字符(bad character)。
 坏字符S没有出现在子字符串中,那么现在可以直接将子字符串整体移到坏字符的后面。
坏字符S没有出现在子字符串中,那么现在可以直接将子字符串整体移到坏字符的后面。 -
还是从子字符串尾部开始比较,P是坏字符,但是它出现在了子字符串中,因此我们向后移动子字符串,使得子字符串中上一次出现的P与坏字符P对齐。

-
移动的位数 = 坏字符的位置 - 在子字符串中上一次出现的位置
比如此处,坏字符P的位置在第6位(从0开始计数),它在子字符串中上一次出现的位置是4,因此向后移动的位数就是2。
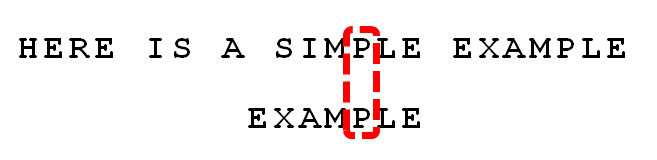 从步骤2到3的过程,坏字符S的位置是6,在子字符串中并未出现,即-1,因此向后移动7位。
从步骤2到3的过程,坏字符S的位置是6,在子字符串中并未出现,即-1,因此向后移动7位。 -
再次从尾部开始比较

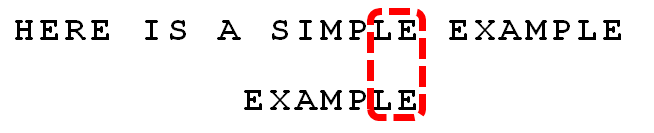
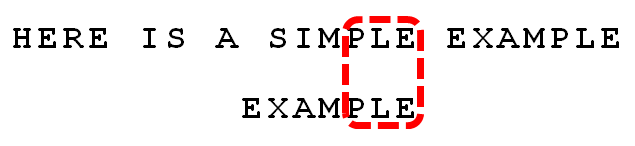
 把这些能与父子符串匹配的后缀称为好后缀(good suffix),E\LE\PLE\MPLE都是好后缀。
把这些能与父子符串匹配的后缀称为好后缀(good suffix),E\LE\PLE\MPLE都是好后缀。
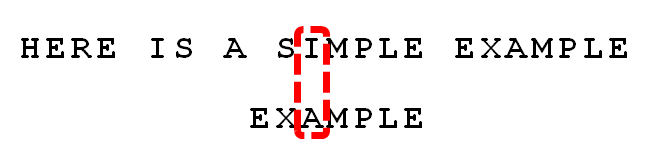 此时,坏字符为I,根据坏字符规则,子字符串下次移动的位数是
此时,坏字符为I,根据坏字符规则,子字符串下次移动的位数是2-(-1)=3。 - 现在有一个新的后移规则好后缀规则:
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
其中这个位置都是指好后缀中最后一个字符的位置。例如现在有子串ABCDAB,末尾的AB是好后缀,它在子串中的位置(及字符B的位置)是5,AB上一次出现的位置为1(上一次出现的AB中字符B在字串中的位置),它向后移动的位数就为4。现在有字串ABCDEF,其中EF为好后缀,F在子串中的位置是5,它在子串中只出现了一次,即上次出现的位置是-1,因此移动的位数为6。
“好后缀”规则注意点: (1)”好后缀”的位置以最后一个字符为准。假定”ABCDEF”的”EF”是好后缀,则它的位置以”F”为准,即5(从0开始计算)。 (2)如果”好后缀”在搜索词中只出现一次,则它的上一次出现位置为 -1。 比如,”EF”在”ABCDEF”之中只出现一次,则它的上一次出现位置为-1(即未出现)。 (3)如果”好后缀”有多个,则除了最长的那个”好后缀”,其他”好后缀”的上一次出现位置必须在头部。比如,假定”BABCDAB”的”好后缀”是”DAB”、”AB”、”B”,请问这时”好后缀”的上一次出现位置是什么?回答是,此时采用的好后缀是”B”,它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个”好后缀”只出现一次,则可以把搜索词改写成如下形式进行位置计算”(DA)BABCDAB”,即虚拟加入最前面的”DA”。
在图中的例子,所有的好后缀E\LE\PLE\MPLE只有E还出现在了字符串头部,因此根据好后缀规则,向后移动的位数是
6-0=6位。 - Boyer-Moore算法根据坏字符和好后缀规则,选择其中移动位数较大的进行移动。
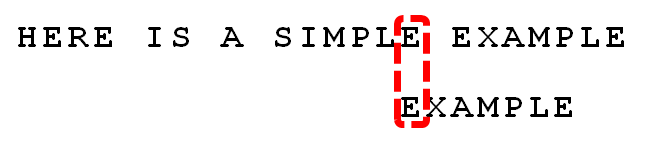 这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
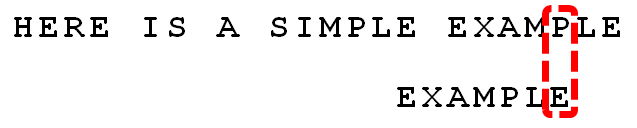 继续从尾部开始比较,”P”与”E”不匹配,因此”P”是”坏字符”。根据”坏字符规则”,后移 6 - 4 = 2位。
继续从尾部开始比较,”P”与”E”不匹配,因此”P”是”坏字符”。根据”坏字符规则”,后移 6 - 4 = 2位。
 从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据”好后缀规则”,后移 6 - 0 = 6位,即头部的”E”移到尾部的”E”的位置。
从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据”好后缀规则”,后移 6 - 0 = 6位,即头部的”E”移到尾部的”E”的位置。
算法实现
function Bm(parent, child) {
let baseP = 0;
while (true) {
let badC = '';
let goodS = '';
let flag = 0;
for (let i = child.length - 1; i >= 0; i--) {
if (child[i] == parent[baseP + i]) {
flag++;
if (flag == child.length) {
return baseP;
}
} else {
badC = parent[baseP + i];
goodS = child.substring(i + 1);
//选择坏字符规则和好后缀规则计算出的较长的后移位数
let b = bad(badC, child, i);
let g = good(goodS, child)
if (b > g) {
baseP += b;
} else {
baseP += g;
}
break;
}
}
if (baseP > parent.length - child.length && baseP < parent.length) baseP = parent.length - child.length; //防止加过的情况
if (baseP == parent.length ) return -1;
}
}
function bad(badC, child, i) {
let sub = child.substring(0, i + 1); //去除好后缀
return i - sub.lastIndexOf(badC);
}
function good(goodS, child) {
if (goodS == "") return 0;
//最长的好后缀至在字串中出现了一次
if (child.lastIndexOf(goodS) == child.indexOf(goodS)) {
let tmp = "";
for (let i = 1; i < goodS.length; i++) {
tmp = goodS.slice(i);
if (child.indexOf(tmp) == 0) {
let str = child.slice(0, child.length - goodS.length);
let newChild = str + child;
return newChild.length - goodS.length;
}
}
return child.length;
} else
//最长的好后缀至在字串中出现了多次
{
let str = child.slice(0, child.length - goodS.length); //去除字串末尾的最长好后缀
let lastIndex = str.lastIndexOf(goodS) + goodS.length - 1; //最长好后缀的最后一个字符上一次出现的位置
return goodS.length - lastIndex;
}
}
小结
- BM算法匹配最差时间复杂度为
O(mn),最佳为O(n/m)
- 下面是从左往右暴力匹配的算法
function Bf(parent,child){
for(let i = 0;i < parent.length; i++){
let flag = 0;
for(let j = 0; j < child.length; j++){
if(parent[i] == child[j]){
i++;
flag++;
}else{
break;
}
}
if(flag == child.length) return i-child.length;
}
return -1;
}
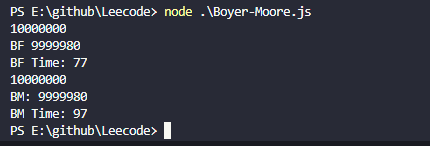
当数据为1000万个字符时,两者匹配最尾部的长度为20的字符串结果如下
 当数据为
当数据为3000万个字符时,两者匹配最尾部的长度为20的字符串结果如下
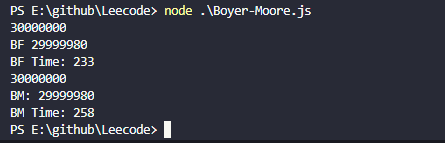
BM和BF算法都是在父字符串上从左往右匹配的,因此增加父字符串的长度不会对对比结果产生较大的影响。
当数据为3000万个字符时,两者匹配最尾部的长度为50的字符串结果如下
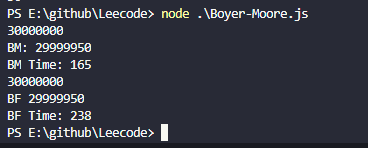 当数据为
当数据为3000万个字符时,两者匹配最尾部的长度为100的字符串结果如下
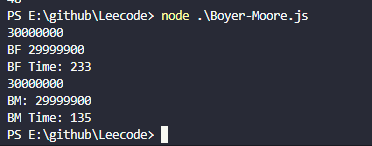 当数据为
当数据为3000万个字符时,两者匹配最尾部的长度为500的字符串结果如下
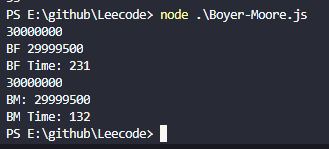
当子字符串的长度增加之后,BM较BF更有优势。